A man was flying over his neighbours lands one dark night when the plane all of a sudden started to have problems. He pulled out his parachute and jumped. Soon he landed in his neighbours cornfield, the only cornfield in the neighbourhood. He knew one thing about this particular cornfield and that was the exact layout of the field. It formed a perfect rectangle, 100m wide and very long, several kilometers. Unfortunately he had lost all sense of direction gliding down the night sky.As he stood there among the corn he thought to himself, how should I walk to be sure to get out of the cornfield as quick as possible, in a worst case scenario?
He is able to walk along any curve he chooses but he has no means of knowing his initial direction. Also, the cornfield is so thick that even if he stands on the very brink of the cornfield he is not aware of it, he must actually step out of it to notice he has succeeded.
Solved by anonymous: Optimal walk is ~227.8m.
The solution is a so called 'yurt' curve.
The optimal value can be found by minimizing
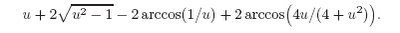
If you place one leg of the yurt in origo and the other leg in u you arrive at the formula above.
12 comments:
I can guarantee a way out after walking 200m. Is there better?
I can say right off that your solution is not correct but
please explain your thoughts and I give you a more precise answer.
Thanks for the effort, you are my number one poster :-)
Actually, I think 200m is too good--that is to say, wrong. :)
I suspect you'll find that your path can, via rotation or shifting, be fit into the field entirely, so that neither edge is intersected.
Looks like Shuusaku beat me to it. :)
It's true, and I don't even have to name my 'solution.' You've guessed it.
I just learned how to use a slide-rule (on Good Math Bad Math). It tells me I can do it in less than 310m. I'll say 315 to be safe, though had I used a calculator, the irrationality would have helped with your cruel edge condition.
Better?
Nice effort :-)
I guess this solution is to walk in a half-circle with radius 100m. This would give a walking length of pi*100m. This is a valid solution but alas not the optimal one.
Let's walk then 2 legs of an equilateral triangle. We need the shortest internal segment (in this case the altitude) to be 100+m, so the side (the walk) should be 200/*sqr(3), followed by a 60 degree turn and a walk of equal length.
115.5 m more than does the trick.
Better?
I see you are making good progress.
Another valid solution and now cut down to a mere 400m/sqrt(3)~231m.
This is a good solution but it can still be improved upon.
Hint?
Puzzle updated with a hint.
228,7M.
Choose the same turning direction for all turnings.
Start walking with radius 100m until you reach the same point as by walking 60m straight forwards. and 20m aside.
Then walk 50m straight forwards.
Turn 106,3 degrees. You will find the angel 73,7degrees in a triangle with the sides 3,4 and 5.
50m straigt and finish with radius 100m as in the beginning
Nice work anonymous!
You have found a very good solution. It still can be improved upon but to go further more elaborate maths is needed. You are on the right track ;)
Post a Comment